Something Strange Happens When You Follow Einstein's Math: A Journey into Black Hole Physics

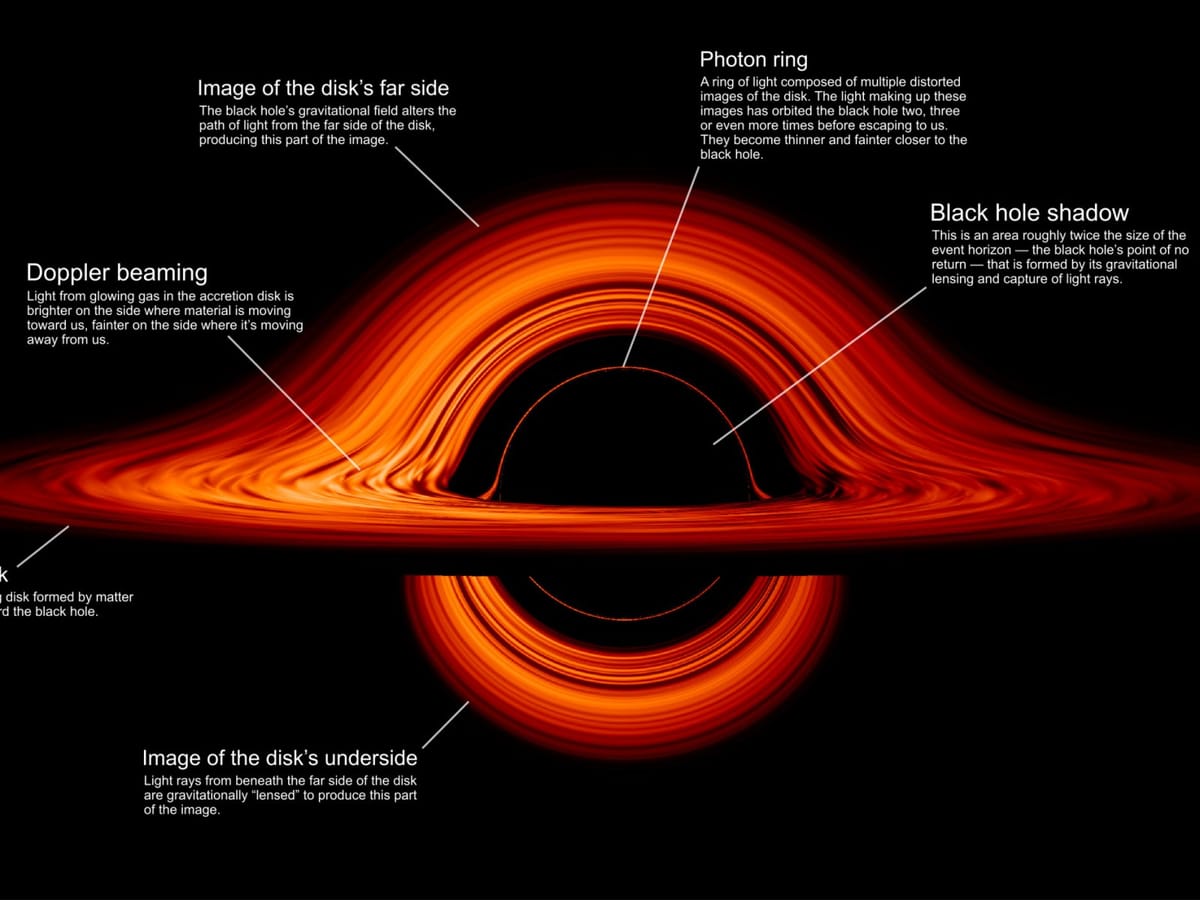
Have you ever wondered what would happen if you fell into a black hole? Would you be crushed instantly, or would something even stranger occur? Thanks to Albert Einstein's groundbreaking work on general relativity [1], we can actually predict what would happen, and the answer is far more bizarre than you might imagine. In this exploration of black hole physics, we'll uncover the mind-bending consequences of Einstein's equations and discover how they reveal some of the most extraordinary phenomena in the universe.

A stunning visualization of a black hole showing the event horizon, accretion disk, and the bending of light around the massive object. The glowing material spiraling into the black hole releases enormous amounts of energy, making these among the brightest objects in the universe.

Table of Contents

1. The Foundation: Einstein's Revolutionary Ideas
2. The Schwarzschild Solution: Describing Black Holes Mathematically
3. The Strange World of Time Dilation
4. Beyond Simple Black Holes: The Kerr Solution
5. Visualizing the Invisible: Spacetime Diagrams
6. The Waterfall Model: A New Way to Think About Gravity
7. Wormholes and Exotic Matter: The Limits of Physics
8. Conclusion: The Ongoing Mystery of Black Holes

The Foundation: Einstein's Revolutionary Ideas

Before we dive into the strange world of black holes, we need to understand the revolutionary ideas that Albert Einstein introduced to the world in 1915 with his theory of general relativity [1]. To appreciate just how radical these ideas were, imagine you're standing on a trampoline. If you place a heavy bowling ball in the center, it creates a depression in the fabric. Now, if you roll a marble across the trampoline, it will curve around the bowling ball, following the shape of the depression.

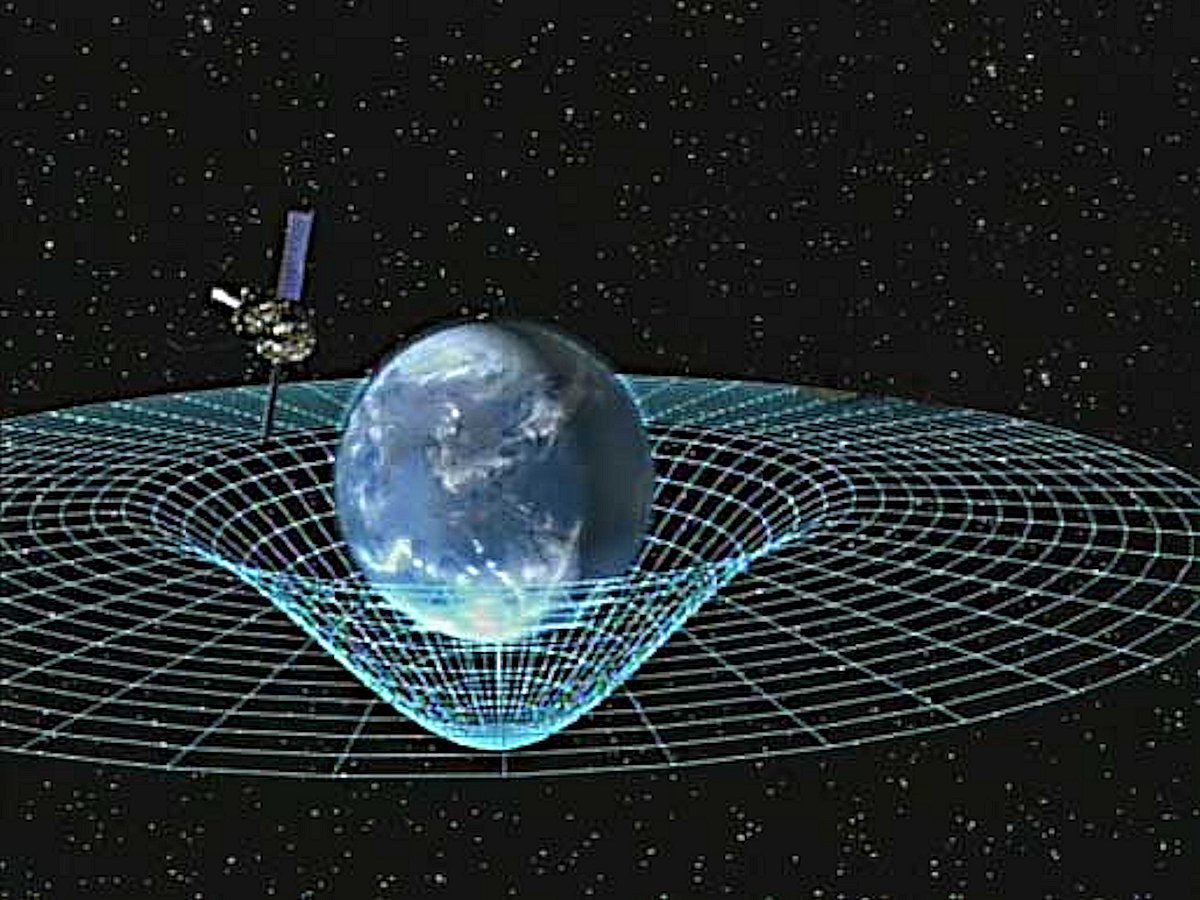
This classic visualization shows how massive objects curve the fabric of spacetime, much like a heavy ball creating a depression in a stretched rubber sheet. Objects follow the curved paths created by this warping of space and time.

Einstein proposed that space and time work in a remarkably similar way. Instead of thinking of gravity as a force that pulls objects together (as Isaac Newton had suggested), Einstein realized that massive objects actually bend the fabric of spacetime itself. This bending is what we experience as gravity. When you drop a ball, it's not being "pulled" toward Earth by some mysterious force. Instead, it's following the curved path through spacetime that Earth's mass has created.

This might sound like science fiction, but Einstein's theory has been tested countless times and has never failed [2]. Every time you use GPS on your phone, you're relying on Einstein's equations to account for the way time runs differently in Earth's gravitational field. Satellites orbiting Earth experience time slightly faster than we do on the surface because they're in a weaker gravitational field. Without correcting for this effect using Einstein's equations, your GPS would be off by several miles within just a few hours.

The mathematical foundation of Einstein's theory is encapsulated in what's known as the Einstein field equations [1]. These equations describe how matter and energy curve spacetime, and how this curvature affects the motion of objects. In their most compact form, they can be written as:

Gμν = 8πTμν

Don't worry if this looks intimidating – the important thing to understand is that this equation connects geometry (the left side, which describes the curvature of spacetime) with matter and energy (the right side). It's saying that matter tells spacetime how to curve, and curved spacetime tells matter how to move.

What makes black holes so fascinating is that they represent an extreme case of this curvature. When enough matter is compressed into a small enough space, the curvature becomes so severe that it creates a region from which nothing, not even light, can escape. This boundary is called the event horizon, and it marks the point of no return for anything falling into the black hole.

But here's where things get really strange. Einstein's equations predict that as you approach a black hole, time itself begins to behave in ways that seem to defy common sense. From the perspective of someone watching from a safe distance, an object falling into a black hole appears to slow down dramatically as it approaches the event horizon. The light from the falling object becomes increasingly redshifted (stretched to longer, redder wavelengths) until it fades away completely. To the distant observer, the falling object appears to freeze at the event horizon, taking an infinite amount of time to cross it.

However, from the perspective of the person falling into the black hole, something completely different happens. They experience time normally and cross the event horizon in a finite amount of time. This apparent contradiction is one of the most mind-bending aspects of black hole physics and illustrates how profoundly Einstein's theory changed our understanding of space and time.

The implications of these ideas extend far beyond black holes themselves. Einstein's theory predicts the existence of gravitational waves – ripples in spacetime itself that travel at the speed of light. These waves were first directly detected in 2015 by the LIGO experiment [3], confirming yet another of Einstein's predictions and opening up an entirely new way of observing the universe. The detected waves came from the collision of two black holes over a billion light-years away, providing us with direct evidence of these cosmic monsters and the extreme physics that governs them.

Understanding Einstein's revolutionary framework is crucial because it provides the mathematical tools we need to explore the strange phenomena that occur near black holes. Without general relativity, we would have no way to predict or understand the bizarre effects we're about to explore. The theory doesn't just describe black holes – it predicts their existence and tells us exactly how they should behave.

As we'll see in the following sections, when we apply Einstein's equations to specific situations involving black holes, we discover phenomena that challenge our intuitions about space, time, and reality itself. The mathematics reveals a universe far stranger and more wonderful than our everyday experience would suggest, where time can slow down, space can be dragged around by spinning objects, and the very fabric of reality can be torn and twisted in ways that seem impossible but are, according to Einstein's equations, inevitable consequences of the laws of physics.

The Schwarzschild Solution: Describing Black Holes Mathematically

Just months after Einstein published his theory of general relativity in 1915, a German physicist named Karl Schwarzschild found the first exact solution to Einstein's field equations [4]. Remarkably, Schwarzschild accomplished this while serving as a soldier on the Russian front during World War I, shortly before his death from an autoimmune disease. His solution describes the spacetime around a spherically symmetric, non-rotating massive object – what we now recognize as the simplest type of black hole.

The Schwarzschild metric provides a mathematical map of spacetime around a non-rotating black hole. This diagram shows how the geometry changes as you approach the event horizon, with the singularity at the center.

The Schwarzschild metric, as it's known, provides a mathematical description of how space and time are curved around a massive object [4]. Think of it as a precise map that tells you how distances and time intervals change as you move closer to or farther from the central mass. Just as a topographic map shows you the elevation changes across a landscape, the Schwarzschild metric shows you how the "elevation" of spacetime changes around a massive object.

The mathematical form of the Schwarzschild metric might look complex, but each part has a clear physical meaning:

ds² = -(1 - 2GM/rc²)c²dt² + (1 - 2GM/rc²)⁻¹dr² + r²dθ² + r²sin²θdφ²

Let's break this down piece by piece. The term ds² represents an infinitesimal interval in spacetime – it combines both spatial distance and time into a single mathematical object. The variables r, θ, and φ are spherical coordinates that describe position in space, while t represents time. The constants G is Newton's gravitational constant, M is the mass of the central object, and c is the speed of light.

The most important part of this equation is the factor (1 - 2GM/rc²), which appears twice with different signs. This factor determines how much spacetime is curved at any given distance r from the central mass. When you're very far from the massive object (when r is much larger than 2GM/c²), this factor approaches 1, and the metric reduces to the familiar flat spacetime of special relativity. But as you get closer to the central mass, this factor becomes smaller, indicating increasingly severe curvature.

The critical distance rs = 2GM/c² is called the Schwarzschild radius, and it marks the location of the event horizon [4]. At this distance, the factor (1 - 2GM/rc²) becomes zero, and the metric exhibits what mathematicians call a singularity. This doesn't mean that physics breaks down at the event horizon – rather, it indicates that the Schwarzschild coordinates become inadequate for describing what happens there, much like how longitude lines converge at the poles of Earth and become undefined.

To understand what the Schwarzschild radius means in practical terms, let's calculate it for some familiar objects. For Earth, with a mass of about 6 × 10²⁴ kilograms, the Schwarzschild radius is approximately 9 millimeters. This means that if you could somehow compress all of Earth's mass into a sphere with a radius smaller than 9 millimeters, it would become a black hole. For the Sun, with a mass of about 2 × 10³⁰ kilograms, the Schwarzschild radius is about 3 kilometers.

These numbers reveal something profound about black holes: they're not necessarily large objects. A black hole with the mass of the Sun would have an event horizon only 6 kilometers across – smaller than most cities. What makes black holes so extreme is not their size, but their incredible density. The matter that forms a black hole is compressed to such an extreme degree that it creates a gravitational field so strong that not even light can escape.

The Schwarzschild solution also reveals the source of the time dilation effects we mentioned earlier. The time component of the metric, which includes the factor (1 - 2GM/rc²), shows that time runs slower in stronger gravitational fields. As you approach the Schwarzschild radius, this factor approaches zero, meaning that time dilation becomes infinite. From the perspective of a distant observer, time appears to stop completely at the event horizon.

But there's a crucial point that often gets overlooked: the Schwarzschild solution describes the spacetime around the black hole, not just the black hole itself. The metric is valid everywhere outside the event horizon, and it smoothly connects to the flat spacetime of special relativity at large distances. This means that if our Sun were suddenly replaced by a black hole of the same mass (don't worry, this can't actually happen), Earth's orbit wouldn't change at all. The gravitational field outside the Schwarzschild radius is identical to that of any other object with the same mass.

The Schwarzschild solution also predicts several phenomena that have since been observed [2]. It describes how light bends as it passes near a massive object, an effect called gravitational lensing. This bending of light was one of the first experimental confirmations of Einstein's theory, observed during a solar eclipse in 1919. The solution also predicts the precession of planetary orbits – a tiny shift in the orientation of elliptical orbits that had been observed in Mercury's orbit but couldn't be explained by Newton's theory.

Perhaps most remarkably, the Schwarzschild solution predicts its own limitations. At the center of the black hole, at r = 0, the curvature becomes infinite – a true singularity where the laws of physics as we know them break down [5]. This singularity is hidden behind the event horizon, preventing us from observing it directly. This is an example of what physicist Roger Penrose called cosmic censorship – the idea that nature conspires to hide singularities from the rest of the universe.

The mathematical elegance of the Schwarzschild solution is striking. From Einstein's complex field equations, Schwarzschild derived a relatively simple formula that describes one of the most extreme objects in the universe. This solution has been tested countless times through astronomical observations, from the orbits of planets in our solar system to the behavior of matter falling into supermassive black holes at the centers of galaxies.

Understanding the Schwarzschild metric is crucial for grasping the more complex black hole solutions we'll explore next. While real black holes in the universe are likely to be rotating (described by the more complex Kerr solution), the Schwarzschild solution provides the foundation for understanding black hole physics. It shows us how mass curves spacetime, how this curvature affects the flow of time, and how the event horizon emerges naturally from Einstein's equations.

The Schwarzschild solution also illustrates a key principle of general relativity: the equivalence of different perspectives. While a distant observer sees time slow down and stop at the event horizon, someone falling into the black hole experiences time normally and crosses the event horizon in finite time. Both perspectives are equally valid – they're simply describing the same physical situation from different reference frames. This relativity of perspective is fundamental to understanding the strange physics of black holes.

The Strange World of Time Dilation

One of the most mind-bending consequences of Einstein's theory is how it reveals that time is not the universal constant we experience in everyday life. Near black holes, time becomes elastic, stretching and compressing in ways that seem to violate our basic intuitions about reality. This phenomenon, called gravitational time dilation, is not just a theoretical curiosity – it's a measurable effect that has profound implications for anyone or anything approaching a black hole.

This illustration shows how time dilation affects clocks at different distances from a black hole. The closer a clock gets to the event horizon, the slower it appears to tick when observed from a safe distance.

To understand gravitational time dilation, imagine two identical clocks: one sitting on your desk and another being lowered toward a black hole. As the second clock gets closer to the black hole, something remarkable happens. If you could observe both clocks simultaneously, you would see that the clock near the black hole begins to tick more slowly compared to the one on your desk. The stronger the gravitational field, the more pronounced this effect becomes.

This isn't because the clock is malfunctioning or because gravity is somehow interfering with its mechanism. Time itself is actually running slower in the stronger gravitational field. This effect occurs because gravity and acceleration are equivalent (a principle Einstein called the equivalence principle), and acceleration affects the flow of time. When you're in a strong gravitational field, you're essentially in a state of constant acceleration, which causes time to dilate.

The mathematical description of this effect comes directly from the Schwarzschild metric we discussed earlier [4]. The time dilation factor is given by the square root of the coefficient of the time term in the metric:

√(1 - 2GM/rc²)

This formula tells us exactly how much time slows down at any distance from a black hole. When you're very far from the black hole (when r is much larger than the Schwarzschild radius), this factor is approximately 1, meaning time runs normally. But as you approach the Schwarzschild radius rs = 2GM/c², this factor approaches zero, meaning time dilation becomes infinite.

Let's put some numbers to this to see how dramatic the effect can be. Consider a black hole with the mass of our Sun (about 2 × 10³⁰ kilograms), which has a Schwarzschild radius of about 3 kilometers. If you were hovering at a distance of 6 kilometers from the center (twice the Schwarzschild radius), time would run about 30% slower than it does far from the black hole. At 4.5 kilometers (1.5 times the Schwarzschild radius), time would run about 50% slower. As you get closer to the event horizon, the time dilation becomes more and more extreme.

This leads to one of the most famous paradoxes in black hole physics. Imagine an astronaut named Alice who decides to fall into a black hole, while her colleague Bob watches from a safe distance. From Bob's perspective, as Alice approaches the event horizon, she appears to slow down dramatically. Her movements become sluggish, her speech becomes deeper and slower, and the light from her spacesuit becomes increasingly redshifted (shifted toward longer, redder wavelengths). Eventually, Alice appears to freeze completely at the event horizon, her image becoming dimmer and redder until it fades away entirely.

From Bob's perspective, Alice never actually crosses the event horizon. She appears to remain frozen there forever, taking an infinite amount of time to cross the boundary. This might lead Bob to conclude that Alice is somehow stuck at the event horizon, unable to proceed further into the black hole.

But Alice's experience is completely different. From her perspective, time flows normally. She doesn't feel herself slowing down, and she doesn't experience any unusual effects as she approaches the event horizon. In fact, if the black hole is large enough, she might not even notice when she crosses the event horizon. She continues falling inward, experiencing normal time, until she eventually reaches the singularity at the center of the black hole.

This apparent contradiction illustrates one of the most profound aspects of Einstein's theory: the relativity of simultaneity. Events that appear simultaneous to one observer may not be simultaneous to another observer in a different reference frame. Bob and Alice are in different reference frames (Bob is stationary far from the black hole, while Alice is in free fall), so they disagree about when certain events occur.

The resolution to this paradox lies in understanding that both perspectives are equally valid. There's no absolute, universal time that determines when Alice "really" crosses the event horizon. From Bob's reference frame, she never crosses it. From Alice's reference frame, she crosses it in finite time. Both descriptions are correct within their respective reference frames.

This time dilation effect has practical implications for space travel and astronomy. If humans ever develop the technology to travel near black holes, time dilation would need to be carefully considered. A journey that takes a few hours for the travelers might correspond to years or even decades passing on Earth. This could be used as a form of time travel to the future – astronauts could travel near a black hole and return to Earth to find that much more time has passed on Earth than during their journey.

Astronomers observe time dilation effects when studying matter falling into black holes. As gas and dust spiral into a black hole, forming what's called an accretion disk, the material closest to the event horizon appears to move more slowly and emit redshifted light. This redshift is partly due to the Doppler effect (the material is moving away from us as it falls in) but also partly due to gravitational time dilation. By measuring these effects, astronomers can study the properties of black holes and test Einstein's predictions.

The time dilation near black holes also affects the emission of light and other electromagnetic radiation. As photons (particles of light) climb out of the gravitational well around a black hole, they lose energy and become redshifted. This gravitational redshift is distinct from the cosmological redshift caused by the expansion of the universe, and it provides another way to test Einstein's theory.

Perhaps most remarkably, the extreme time dilation near black holes means that the event horizon acts as a kind of temporal boundary. From the perspective of the outside universe, nothing ever quite reaches the event horizon – it just gets closer and closer, slowing down more and more, until it effectively freezes in time. This suggests that, from the outside perspective, black holes might be better thought of as "frozen stars" – objects that are perpetually in the process of collapsing but never quite finish the collapse.

However, this doesn't mean that black holes don't grow. As more matter falls toward a black hole, it adds to the mass and energy of the system, causing the event horizon to expand outward. The new matter doesn't need to cross the old event horizon – instead, the event horizon expands to encompass the new matter. This process allows black holes to grow while maintaining the property that, from the outside perspective, nothing ever crosses the event horizon.

The study of time dilation near black holes has also led to insights about the nature of information and quantum mechanics. If information falling into a black hole appears to freeze at the event horizon from the outside perspective, what happens to that information? This question has led to the development of new theories about black hole thermodynamics [6] and the holographic principle, which suggests that all the information about the interior of a black hole might be encoded on its surface.

Understanding time dilation is crucial for grasping the full strangeness of black hole physics. It shows us that time is not the fixed, universal backdrop that our everyday experience suggests, but rather a dynamic aspect of spacetime that can be stretched, compressed, and manipulated by gravity. This flexibility of time is one of the most profound insights of Einstein's theory and one of the key features that makes black holes such fascinating objects to study.

Beyond Simple Black Holes: The Kerr Solution

While the Schwarzschild solution provides a beautiful description of non-rotating black holes, the real universe is far more dynamic. Most black holes in nature are expected to be spinning, sometimes at incredible speeds approaching the maximum possible rotation rate. In 1963, New Zealand mathematician Roy Kerr found the solution to Einstein's equations that describes these rotating black holes [7], revealing phenomena even stranger than those predicted by the simpler Schwarzschild case.

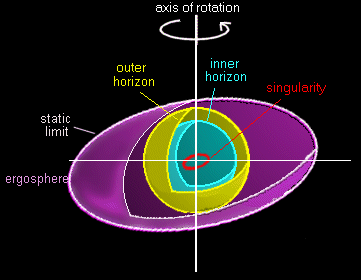
This animation shows the structure of a rotating (Kerr) black hole, including the ergosphere (the region where spacetime is dragged around by the black hole's rotation) and the two event horizons. The rotation creates a complex geometry that differs dramatically from non-rotating black holes.

The Kerr solution describes a black hole that rotates around a central axis, much like a spinning top [7]. This rotation fundamentally changes the structure of spacetime around the black hole, creating new regions and phenomena that don't exist around non-rotating black holes. The mathematics of the Kerr solution is significantly more complex than the Schwarzschild case, but the physical insights it provides are profound and have revolutionized our understanding of black hole physics.

When a massive object spins, it drags spacetime along with it in an effect called frame-dragging or the Lense-Thirring effect [8]. Imagine spacetime as a thick fluid, like honey, and the spinning black hole as a spoon stirring through it. The rotation of the black hole causes nearby spacetime to swirl around the central axis, creating a kind of gravitational whirlpool. This effect becomes more pronounced closer to the black hole and reaches extreme levels near the event horizon.

The frame-dragging effect predicted by general relativity has been measured in the solar system using satellites orbiting Earth. The Gravity Probe B experiment, launched in 2004, used incredibly precise gyroscopes to measure how Earth's rotation drags spacetime around it [9]. While the effect is tiny – only about 39 milliarcseconds per year – it was successfully detected, providing another confirmation of Einstein's theory.

The Kerr solution reveals that rotating black holes have not one, but two event horizons [7]. The outer event horizon is similar to the event horizon of a Schwarzschild black hole, but there's also an inner event horizon closer to the center. Between these two horizons lies a region where the physics becomes even more exotic than in the Schwarzschild case. However, the most remarkable feature of the Kerr solution is the discovery of a region called the ergosphere.

The ergosphere is a region outside the outer event horizon where the frame-dragging effect becomes so strong that nothing can remain stationary relative to distant observers [7]. Even if you fired your rocket engines at maximum power, you couldn't hover in a fixed position within the ergosphere – you would be dragged around the black hole by the swirling spacetime itself. This doesn't mean you're necessarily falling into the black hole; you could still escape from the ergosphere, but you can't avoid being dragged around the central axis.

The boundary of the ergosphere is called the static limit, and it's located at a distance from the center given by:

r = GM/c² + √((GM/c²)² - a²cos²θ)

Here, a represents the angular momentum per unit mass of the black hole (related to how fast it's spinning), and θ is the angle from the rotation axis. Notice that the ergosphere is not spherical – it's flattened at the poles and bulges out at the equator, reflecting the rotational symmetry of the system.

The existence of the ergosphere leads to one of the most remarkable predictions of black hole physics: the possibility of extracting energy from a rotating black hole through a process called the Penrose mechanism, named after physicist Roger Penrose who first described it [10]. Here's how it works: imagine you drop an object into the ergosphere and then split it into two pieces. If you arrange the split carefully, one piece can fall into the black hole while the other escapes with more energy than the original object had. The extra energy comes from the rotational energy of the black hole itself.

This might sound like it violates conservation of energy, but it doesn't. The piece that falls into the black hole actually has negative energy as measured by distant observers. When this negative energy is absorbed by the black hole, it reduces the black hole's total mass and angular momentum. Meanwhile, the escaping piece carries away positive energy, more than the original object possessed. The net result is that energy is extracted from the black hole's rotation, causing it to spin more slowly.

The Penrose mechanism has profound implications for astrophysics [10]. In principle, a sufficiently advanced civilization could use this process to extract enormous amounts of energy from rotating black holes. Some scientists have speculated that this might explain the incredible energy output of quasars and other active galactic nuclei, where matter falling into supermassive black holes releases more energy than entire galaxies of stars.

The mathematical description of the Kerr metric is considerably more complex than the Schwarzschild case, involving elliptic coordinates and functions that don't have simple closed forms. However, the key insight is that the rotation parameter a determines how much the black hole deviates from the spherically symmetric Schwarzschild case. When a = 0 (no rotation), the Kerr metric reduces to the Schwarzschild metric. As a increases, the effects of frame-dragging become more pronounced, and the ergosphere becomes larger.

There's a maximum possible value for the rotation parameter, given by a = GM/c² [7]. This corresponds to an extremal Kerr black hole, spinning at the maximum possible rate. If a black hole were to spin faster than this, the event horizons would disappear, exposing the central singularity to the outside universe – a situation that most physicists believe is forbidden by cosmic censorship. Real black holes are expected to spin at rates somewhat below this maximum, typically with a between 0.5 and 0.99 times the maximum value.

Near black holes, the frame-dragging effect is much more dramatic than around Earth. Matter in the accretion disk around a rotating black hole is forced to orbit in the same direction as the black hole's rotation [8]. This can lead to the formation of jets – narrow beams of high-energy particles that are ejected from the vicinity of the black hole at speeds approaching the speed of light. These jets are among the most energetic phenomena in the universe and can extend for millions of light-years from their source.

The Kerr solution also predicts that the singularity at the center of a rotating black hole is not a point (as in the Schwarzschild case) but rather a ring [7]. This ring singularity has led to speculation about the possibility of traveling through the black hole to emerge in another region of spacetime, or even another universe entirely. However, such journeys would likely be impossible due to the extreme tidal forces and instabilities that would destroy any material object long before it could reach the singularity.

The study of Kerr black holes has also revealed important connections between black hole physics and thermodynamics [6]. Rotating black holes have both mass and angular momentum, and they can be assigned a temperature and entropy. The laws of black hole thermodynamics, developed by physicists like Stephen Hawking and Jacob Bekenstein, show that black holes behave in many ways like ordinary thermodynamic systems, with the event horizon area playing the role of entropy.

Perhaps most remarkably, the Kerr solution shows that the interior of a rotating black hole contains regions where the normal causal structure of spacetime breaks down [7]. Inside the inner event horizon, there are closed timelike curves – paths through spacetime that loop back on themselves, potentially allowing for time travel to the past. However, these regions are likely unstable and would be destroyed by quantum effects, preventing any practical time travel scenarios.

The Kerr solution represents one of the most beautiful and complex exact solutions to Einstein's field equations. It shows how rotation fundamentally changes the nature of spacetime around a massive object, creating new phenomena like the ergosphere and frame-dragging that have no analogue in Newtonian gravity. As we continue to observe black holes with increasingly sophisticated instruments, the predictions of the Kerr solution provide a crucial framework for understanding these cosmic monsters and the extreme physics that governs their behavior.

Visualizing the Invisible: Spacetime Diagrams

One of the greatest challenges in understanding black holes is that they involve phenomena that are completely outside our everyday experience. How do you visualize something where space and time are curved, where the normal rules of causality break down, and where the very concepts of "inside" and "outside" become ambiguous? Physicists have developed several ingenious ways to represent these complex spacetime geometries using diagrams that reveal the hidden structure of black holes.

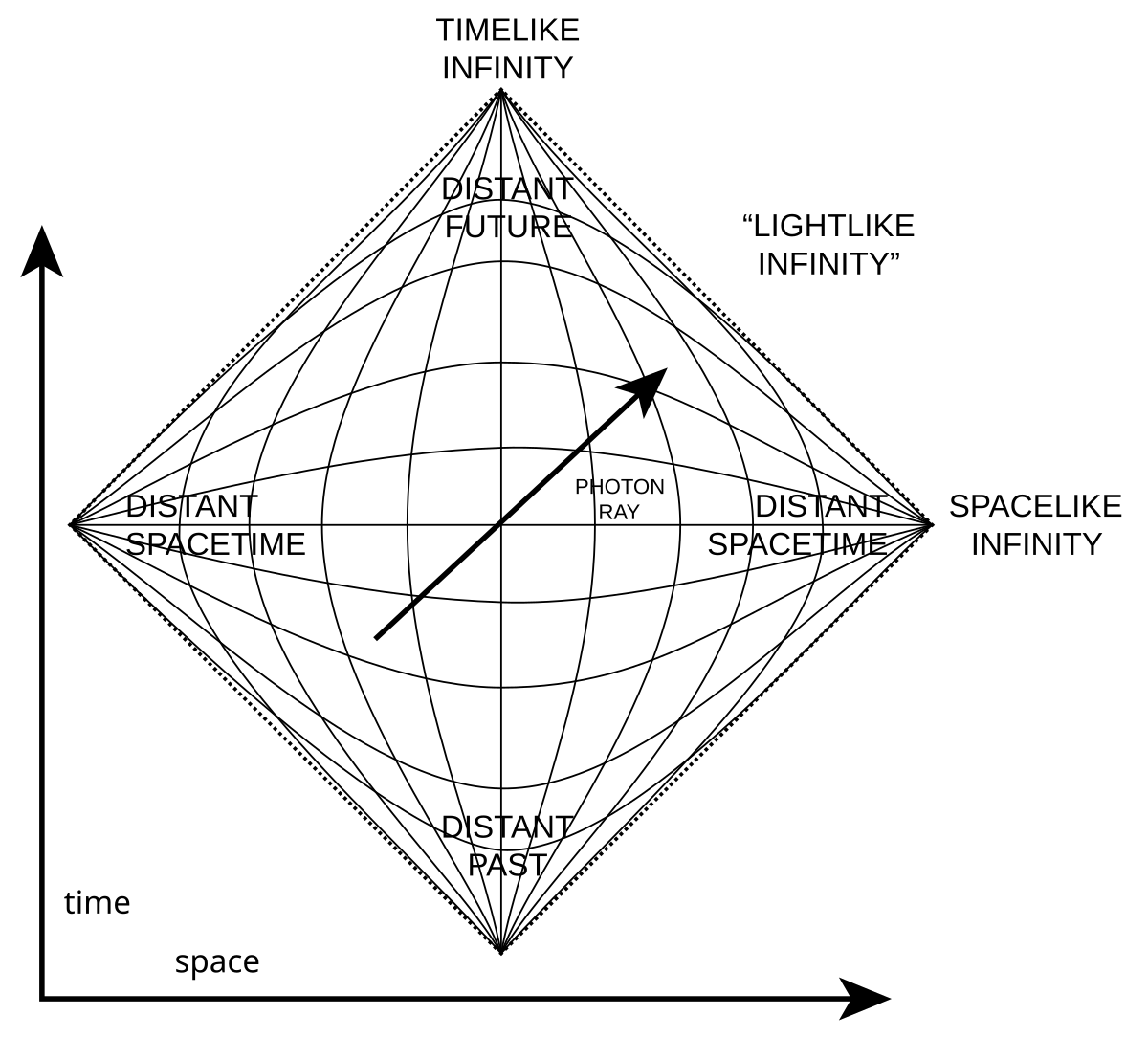
A Penrose diagram for a black hole spacetime. The diamond shape represents the entire spacetime, with the event horizon as a diagonal line and the singularity as the jagged line at the top. Light rays always travel at 45-degree angles in these diagrams.

The most powerful of these visualization tools are Penrose diagrams and Kruskal-Szekeres diagrams [11]. These aren't just pretty pictures – they're precise mathematical representations that capture the essential features of black hole spacetime in a way that makes the physics clear and intuitive. By learning to read these diagrams, we can understand phenomena that would otherwise be impossible to visualize or comprehend.

Let's start with Penrose diagrams, named after physicist Roger Penrose who developed them in the 1960s [11]. The key insight behind Penrose diagrams is that we can represent the entire spacetime geometry of a black hole on a finite piece of paper by using a clever mathematical transformation. This transformation compresses infinite distances and infinite times into finite regions while preserving the essential causal structure of spacetime.

In a Penrose diagram, the entire history of spacetime is represented as a diamond-shaped region. Light rays always travel at 45-degree angles (when drawn to the proper scale), making it easy to see which events can influence which other events. The boundaries of the diagram represent infinity – spatial infinity (where you'd end up if you traveled infinitely far in any spatial direction) and timelike infinity (the infinite future and past).

For a black hole, the Penrose diagram reveals several crucial features [11]. The event horizon appears as a diagonal line running from the bottom left to the top right of the diagram. Everything to the left of this line is the exterior region, where escape is possible. Everything to the right is the interior region, where escape is impossible. The singularity at the center of the black hole appears as a jagged line at the top of the interior region, representing the fact that it's a moment in time rather than a place in space.

This last point is particularly important and often misunderstood. In popular culture, black hole singularities are often depicted as places – perhaps a point in the center of the black hole where you might arrive if you fell in. But the Penrose diagram shows that the singularity is actually a moment in time [5]. If you fall into a black hole, you don't travel to the singularity; you travel until the singularity, at which point your journey through time comes to an end.

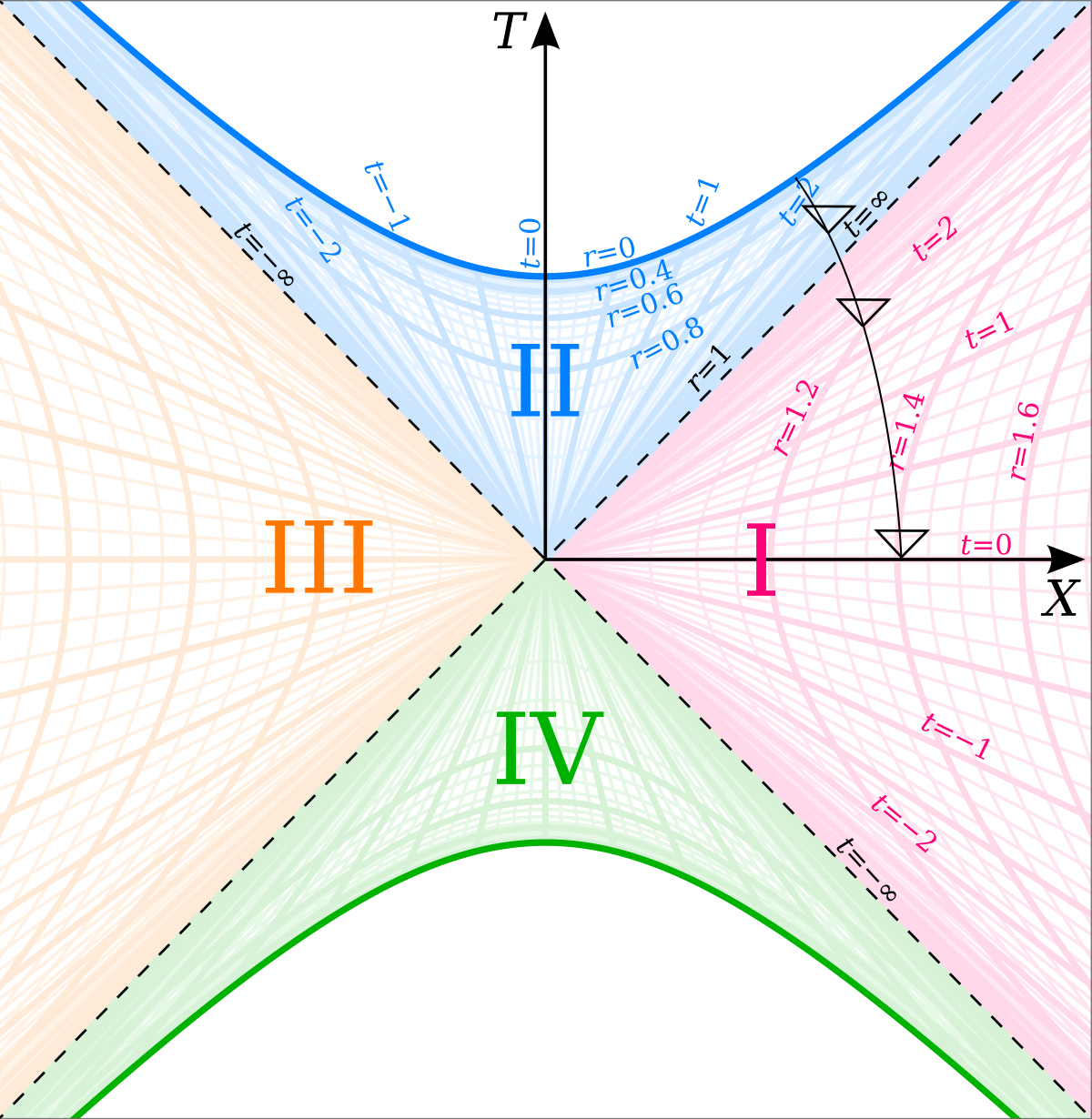
A Kruskal-Szekeres diagram showing the complete spacetime structure of an eternal black hole. The four regions (I-IV) represent different parts of spacetime, with Region I being our normal exterior universe and Region II being the black hole interior.

Kruskal-Szekeres diagrams provide another powerful way to visualize black hole spacetime [12]. These diagrams use different coordinates that have the advantage of being well-behaved at the event horizon, unlike the standard Schwarzschild coordinates which become singular there. In Kruskal-Szekeres coordinates, the event horizon appears as straight lines, and the entire spacetime can be divided into four distinct regions.

Region I is the exterior region, where we normally live. Region II is the interior of the black hole, where anything that crosses the event horizon ends up. But the Kruskal-Szekeres diagram reveals two additional regions that don't exist in the Schwarzschild coordinates [12]. Region III is another exterior region, completely disconnected from Region I. Region IV is a "white hole" – the time-reverse of a black hole, where matter can only exit, never enter.

The complete Kruskal-Szekeres diagram describes what's called an eternal black hole – a black hole that has existed forever and will exist forever [12]. This is a mathematical idealization; real black holes form from the collapse of massive stars and have a more complex structure. However, the eternal black hole solution reveals important features about the geometry of spacetime that apply more generally.

One of the most remarkable features revealed by the Kruskal-Szekeres diagram is the existence of an Einstein-Rosen bridge, more commonly known as a wormhole [13]. The diagram shows that Regions I and III are connected through the interior of the black hole. In principle, you could travel from one exterior region to the other by passing through the black hole. However, this journey would be one-way and would end at the singularity, making it impossible to actually use the wormhole for travel between the two regions.

These diagrams also help us understand the resolution to the time dilation paradox we discussed earlier. In the Kruskal-Szekeres coordinates, an infalling observer crosses the event horizon in finite coordinate time, while a distant observer sees the infalling observer approach the horizon asymptotically [12]. Both descriptions are correct – they're simply using different coordinate systems to describe the same physical situation.

The power of these spacetime diagrams extends beyond just black holes. Similar techniques can be used to visualize the spacetime geometry around other exotic objects, such as wormholes, cosmic strings, and even the entire universe. Penrose diagrams of cosmological spacetimes show the Big Bang as a spacelike boundary at the bottom of the diagram and reveal the causal structure of the expanding universe.

For rotating black holes described by the Kerr solution, the spacetime diagrams become even more complex [7]. The Kerr black hole has two event horizons, and the region between them has unusual properties. In this region, there are closed timelike curves – paths through spacetime that loop back on themselves, potentially allowing for time travel to the past. However, these regions are likely unstable and would be destroyed by quantum effects in any realistic scenario.

The development of these visualization techniques has been crucial for advancing our understanding of black hole physics. Before Penrose and Kruskal-Szekeres developed their coordinate systems, physicists struggled to understand what happened at the event horizon. The original Schwarzschild coordinates suggested that something dramatic occurred there, but the new coordinates revealed that the event horizon is actually a smooth, well-behaved surface from the perspective of an infalling observer.

These diagrams have also been essential for understanding black hole thermodynamics and the information paradox [6]. By clearly showing the causal structure of black hole spacetime, they help us understand how information might be preserved when matter falls into a black hole and how Hawking radiation might carry information back out.

Modern research in black hole physics continues to rely heavily on these visualization techniques. When physicists study the collision of two black holes (the kind of event that produces gravitational waves [3]), they use sophisticated versions of these diagrams to understand how the spacetime geometry evolves during the merger. When they investigate the quantum properties of black holes, they use these diagrams to understand how quantum fields behave in curved spacetime.

Perhaps most importantly, these diagrams teach us that our intuitive notions of space and time break down in extreme gravitational fields. The idea that space and time are separate, absolute entities is revealed to be an approximation that works well in weak gravitational fields but fails completely near black holes. Instead, space and time are unified into a single, dynamic entity – spacetime – that can be curved, twisted, and even torn by the presence of matter and energy.

The beauty of Penrose and Kruskal-Szekeres diagrams is that they make these abstract concepts concrete and visual. They transform the complex mathematics of general relativity into pictures that reveal the hidden structure of reality. By learning to read these diagrams, we gain insight into some of the most profound questions in physics: What is the nature of space and time? How do cause and effect work in extreme gravitational fields? What happens at the boundary between the known and the unknowable?

These visualization techniques continue to evolve as our understanding of black holes deepens. New types of diagrams are being developed to represent the quantum properties of black holes, the effects of Hawking radiation [14], and the complex dynamics of black hole mergers. Each new diagram reveals another aspect of the rich, strange world that Einstein's equations describe – a world where the familiar becomes exotic and the impossible becomes inevitable.

The Waterfall Model: A New Way to Think About Gravity

While mathematical equations and spacetime diagrams provide precise descriptions of black hole physics, they can be difficult to visualize intuitively. To bridge this gap, physicists have developed what's known as the "waterfall model" or "river model" of spacetime [15]. This model provides a remarkably intuitive way to understand how gravity works and why black holes behave the way they do, transforming abstract mathematical concepts into something we can visualize and feel.

The waterfall model visualizes spacetime as flowing like a river toward massive objects. Near black holes, this flow becomes so strong that even light cannot swim upstream against it, explaining why nothing can escape from inside the event horizon.

The waterfall model starts with a simple but profound insight: instead of thinking of gravity as a force that pulls objects together, we can think of spacetime itself as flowing like a river toward massive objects [15]. In this picture, objects don't fall because they're being pulled – they fall because they're being carried along by the flow of spacetime itself. This flowing spacetime is not just a metaphor; it's a precise mathematical description that emerges naturally from Einstein's equations.

To understand how this works, imagine you're in a boat on a river. Even if you turn off your engine and try to remain stationary, the current will carry you downstream. The only way to maintain your position is to fire up your engine and travel upstream at exactly the speed of the current. If the current becomes too strong, even your most powerful engine won't be able to overcome it, and you'll inevitably be swept downstream.

Spacetime around a massive object behaves in a remarkably similar way [15]. The presence of mass causes spacetime to "flow" inward toward the center of the object. Objects in this flowing spacetime are carried along by the flow, which we experience as gravitational attraction. To remain at a fixed distance from a massive object, you need to accelerate outward at just the right rate to counteract the inward flow of spacetime.

Near a black hole, this spacetime flow becomes extreme. Far from the black hole, the flow is gentle – you can easily maintain your position with a small amount of acceleration. But as you get closer to the black hole, the flow becomes stronger and stronger. At the event horizon, the flow of spacetime reaches the speed of light [15]. This is why nothing can escape from inside a black hole: even light, traveling at the maximum possible speed, is swept inward by the flow of spacetime.

The waterfall model provides an intuitive explanation for many of the strange phenomena we've discussed. Consider the time dilation effect: in the waterfall model, time dilation occurs because clocks are being carried along by the flowing spacetime. A clock deeper in the gravitational well is in a region where spacetime is flowing faster, and this affects the rate at which time passes. From the perspective of someone in the faster-flowing region, time appears normal, but to an outside observer, the clock appears to run slowly.

The model also explains why objects appear to freeze at the event horizon when viewed from a distance. In the waterfall model, light from an object approaching the event horizon has to "swim upstream" against the flow of spacetime to reach a distant observer. As the object gets closer to the event horizon, the spacetime flow becomes stronger, making it increasingly difficult for light to escape. At the event horizon, the flow reaches the speed of light, so light from the object can barely escape, becoming infinitely redshifted in the process.

From the perspective of someone falling into the black hole, however, the experience is quite different. They're being carried along by the flow of spacetime, so they don't feel the effects of the flow directly. To them, spacetime appears stationary, and they cross the event horizon in finite time without experiencing anything unusual (assuming the black hole is large enough that tidal forces aren't significant).

The waterfall model becomes even more interesting when we consider rotating black holes [15]. In this case, spacetime doesn't just flow inward – it also swirls around the central axis due to the frame-dragging effect we discussed earlier [8]. This creates a kind of gravitational whirlpool, where spacetime spirals inward like water going down a drain. The ergosphere corresponds to the region where this swirling flow becomes so strong that nothing can remain stationary relative to distant observers.

This swirling flow of spacetime around rotating black holes has observable consequences. Matter in the accretion disk around a black hole is forced to orbit in the same direction as the black hole's rotation because it's being carried along by the swirling spacetime. This can lead to the formation of jets – narrow beams of high-energy particles that are ejected along the rotation axis of the black hole.

The waterfall model also provides insight into how black holes can extract energy from infalling matter. In the model, the kinetic energy of matter falling through the flowing spacetime can be converted into other forms of energy, such as heat and electromagnetic radiation. This is why accretion disks around black holes are among the most luminous objects in the universe – they're converting the gravitational potential energy of infalling matter into light and heat with incredible efficiency.

One of the most remarkable aspects of the waterfall model is that it makes the connection between gravity and thermodynamics more intuitive [6]. In the model, the event horizon acts like a one-way membrane: matter and energy can flow in, but nothing can flow out. This is similar to the behavior of a thermodynamic system at equilibrium, where entropy can only increase. The area of the event horizon in the waterfall model corresponds to the entropy of the black hole, and the surface gravity (related to the strength of the spacetime flow at the horizon) corresponds to the temperature.

The waterfall model has also been useful for understanding Hawking radiation – the quantum mechanical process by which black holes slowly evaporate [14]. In the model, quantum fluctuations near the event horizon can create particle-antiparticle pairs. If one particle falls into the black hole while the other escapes, the escaping particle carries away energy, causing the black hole to lose mass. The waterfall model helps visualize how this process works and why it leads to a thermal spectrum of radiation.

Physicists have even created laboratory analogues of the waterfall model using actual flowing fluids [16]. In these "analogue gravity" experiments, researchers create flows of water or other fluids that mimic the spacetime flow around black holes. Sound waves in these fluids behave similarly to light waves in curved spacetime, allowing scientists to study black hole physics in the laboratory. These experiments have provided new insights into Hawking radiation and other quantum effects near black holes.

The waterfall model has limitations, of course. It's a simplified picture that captures many important features of black hole physics but doesn't include all the complexities of the full mathematical description. For instance, the model doesn't naturally incorporate the effects of quantum mechanics or the detailed structure of spacetime near the singularity. However, as an intuitive guide to understanding black hole physics, it's remarkably powerful and accurate.

Perhaps most importantly, the waterfall model helps us understand that gravity is not a force in the traditional sense, but rather a manifestation of the geometry of spacetime itself [1]. This insight, which lies at the heart of Einstein's theory, is often difficult to grasp from the mathematical formalism alone. The waterfall model makes this abstract concept concrete and intuitive, showing us that we live in a universe where space and time are dynamic, flowing entities that can be shaped and molded by the presence of matter and energy.

The model also illustrates one of the most profound insights of modern physics: that seemingly different phenomena can have deep underlying connections. The flow of spacetime around a black hole, the behavior of fluids in a laboratory, and the thermodynamic properties of gases all share similar mathematical structures [16]. This universality suggests that there are fundamental principles governing the behavior of complex systems, whether they involve gravity, fluid dynamics, or thermodynamics.

As our understanding of black holes continues to evolve, the waterfall model remains a valuable tool for developing intuition about these exotic objects. It provides a bridge between the abstract mathematics of general relativity and our everyday experience of flowing fluids, making the strange physics of black holes more accessible and understandable. In a universe where space and time can be curved, twisted, and torn, the waterfall model gives us a way to visualize and comprehend phenomena that would otherwise be beyond our imagination.

Wormholes and Exotic Matter: The Limits of Physics

Einstein's equations are remarkably permissive when it comes to the kinds of spacetime geometries they allow. While we've focused primarily on black holes, the equations also permit other exotic solutions, including wormholes – hypothetical tunnels through spacetime that could potentially connect distant regions of the universe or even different universes entirely [17]. However, as we'll see, the physics required to create and maintain such structures pushes against some of the most fundamental principles of physics, revealing the delicate balance between mathematical possibility and physical reality.

A wormhole, formally known as an Einstein-Rosen bridge, is a solution to Einstein's field equations that describes a tunnel-like connection between two separate regions of spacetime [13]. Imagine taking a sheet of paper and folding it so that two distant points touch, then poking a hole through both layers. The hole represents a wormhole – a shortcut that allows you to travel between the two points without traversing the full distance across the surface of the paper.

The mathematical description of a wormhole is actually quite similar to that of a black hole, but with a crucial difference. While a black hole has an event horizon that prevents escape, a wormhole has what's called a "throat" – a narrow region that connects two asymptotically flat regions of spacetime [17]. In principle, you could enter one mouth of the wormhole, travel through the throat, and emerge from the other mouth in a completely different location.

The simplest wormhole solution, discovered by Einstein and Nathan Rosen in 1935, is actually just a different way of looking at the Schwarzschild black hole solution [13]. The complete Schwarzschild geometry, when properly extended, describes not just a black hole but also a white hole (the time-reverse of a black hole) connected by a bridge through spacetime. However, this Einstein-Rosen bridge is not traversable – anything that enters it will be crushed by the singularity before it can emerge on the other side.

To create a traversable wormhole – one that you could actually travel through – requires something much more exotic [17]. The throat of the wormhole must be held open against the natural tendency of spacetime to collapse. This requires a form of matter with very unusual properties: it must have negative energy density as measured by certain observers. This hypothetical substance is called exotic matter, and its existence would violate what physicists call the weak energy condition.

The weak energy condition is one of several energy conditions that physicists believe should be satisfied by all forms of matter and energy in the universe [17]. It states that the energy density of matter, as measured by any observer, should always be non-negative. This seems like a reasonable requirement – after all, we don't encounter negative energy in our everyday experience. However, the requirement for exotic matter to stabilize wormholes suggests that traversable wormholes might be impossible to create or maintain.

The mathematical requirements for exotic matter become clear when we examine the Einstein field equations for a wormhole geometry [17]. To keep the throat of the wormhole open, the stress-energy tensor (which describes the distribution of matter and energy) must have negative eigenvalues in certain directions. This means that the matter threading the wormhole must exert a negative pressure – it must pull spacetime apart rather than pushing it together, as ordinary matter does.

To understand why this is so unusual, consider what happens when you try to stretch a rubber band. The rubber exerts a restoring force that tries to return it to its original length. Ordinary matter behaves similarly – it resists compression and expansion in ways that tend to curve spacetime in predictable directions. Exotic matter, by contrast, would behave like a rubber band with negative tension – it would actively try to stretch itself apart, creating a repulsive gravitational effect.

The amount of exotic matter required to stabilize a wormhole depends on the size and geometry of the wormhole, but even for relatively small wormholes, the requirements are staggering [17]. For a wormhole with a throat radius of about one meter, you would need exotic matter with an energy density comparable to that of an atomic nucleus, but with the opposite sign. The total amount of exotic matter required would be enormous – potentially more than the mass of the Sun, but with negative energy.

Some physicists have proposed that quantum effects might provide a source of exotic matter [18]. In quantum field theory, the vacuum is not empty but filled with virtual particles that constantly appear and disappear. Under certain circumstances, these quantum fluctuations can produce regions of negative energy density. The Casimir effect, which has been experimentally verified, demonstrates that quantum fields can indeed produce negative energy densities between closely spaced conducting plates.

However, there are severe limitations on how much negative energy can be accumulated and how long it can be maintained [18]. Quantum inequalities, derived from the fundamental principles of quantum mechanics, place strict bounds on the magnitude and duration of negative energy densities. These inequalities suggest that while small amounts of exotic matter might be possible, the vast quantities required to stabilize macroscopic wormholes are likely impossible to achieve.

Even if exotic matter could somehow be obtained, maintaining a stable wormhole would present additional challenges [17]. Wormholes are inherently unstable – any small perturbation, such as a single photon passing through the throat, can cause the wormhole to collapse. This instability is a consequence of the same physics that makes black holes stable: spacetime has a natural tendency to develop event horizons and singularities when matter and energy are concentrated in small regions.

The instability of wormholes has led some physicists to propose that advanced civilizations might be able to stabilize them using feedback mechanisms [17]. Imagine a system that constantly monitors the geometry of the wormhole and injects exotic matter as needed to counteract any tendency toward collapse. However, such a system would require technology far beyond anything we can currently imagine, and it's unclear whether the fundamental laws of physics would permit such precise control over spacetime geometry.

Despite these challenges, the study of wormholes has led to important insights about the nature of spacetime and the limits of general relativity. Wormholes provide a testing ground for exploring the relationship between gravity and quantum mechanics, and they've inspired new approaches to understanding black hole thermodynamics and the information paradox [6].

The possibility of wormholes has also raised fascinating questions about causality and time travel [19]. If wormholes could be created and manipulated, they might potentially be used to construct closed timelike curves – paths through spacetime that loop back on themselves, allowing for travel to the past. However, such scenarios typically lead to paradoxes (like the famous grandfather paradox) that suggest fundamental inconsistencies in the laws of physics.

Some physicists have proposed that the universe has built-in mechanisms to prevent such paradoxes [19]. The chronology protection conjecture, suggested by Stephen Hawking, proposes that the laws of physics conspire to prevent the formation of closed timelike curves. Quantum effects, which we've largely ignored in our discussion of classical general relativity, might play a crucial role in enforcing this protection.

The study of wormholes has also contributed to our understanding of the holographic principle and the AdS/CFT correspondence – advanced topics in theoretical physics that suggest deep connections between gravity and quantum field theory [20]. In these frameworks, wormholes in the bulk spacetime correspond to quantum entanglement between different regions of the boundary theory, providing new insights into the nature of spacetime itself.

Recent developments in quantum information theory have revealed surprising connections between wormholes and quantum entanglement [20]. The ER=EPR conjecture, proposed by physicists Juan Maldacena and Leonard Susskind, suggests that quantum entanglement and wormholes might be two different descriptions of the same physical phenomenon. If true, this would mean that the quantum entanglement that exists between particles in our everyday world might actually be manifestations of microscopic wormholes in spacetime.

While traversable wormholes remain highly speculative, their study continues to push the boundaries of our understanding of physics [17]. They represent the extreme limits of what Einstein's equations allow, revealing the delicate balance between mathematical possibility and physical reality. Even if wormholes turn out to be impossible in practice, the attempt to understand them has led to new insights about spacetime, quantum mechanics, and the fundamental structure of reality.

The quest to understand wormholes also illustrates one of the most important aspects of theoretical physics: the exploration of mathematical possibilities, even when they seem to violate our intuitions about how the world should work [1]. Einstein's equations permit wormholes, just as they permit black holes, and both solutions have taught us profound lessons about the nature of space and time. Whether or not wormholes actually exist in nature, they serve as powerful tools for exploring the limits of physics and pushing our understanding of the universe to its very foundations.

In the end, the study of wormholes reminds us that the universe described by Einstein's equations is far stranger and more wonderful than our everyday experience suggests [1]. While the practical challenges of creating traversable wormholes may be insurmountable, the theoretical exploration of these exotic spacetime geometries continues to reveal new aspects of the deep structure of reality, showing us that even the most speculative ideas in physics can lead to genuine insights about the nature of space, time, and existence itself.

Conclusion: The Ongoing Mystery of Black Holes

As we reach the end of our journey through the strange world of black hole physics, it's worth reflecting on just how far we've traveled from our everyday understanding of space and time. We began with Einstein's revolutionary insight that gravity is not a force but a manifestation of curved spacetime [1], and we've seen how this simple idea leads to phenomena that seem to violate our most basic intuitions about reality.

We've discovered that time is not the universal constant we experience in daily life, but rather a flexible dimension that can be stretched and compressed by gravity. We've seen how the event horizon of a black hole acts as a one-way membrane in spacetime, allowing matter and energy to flow in but never out. We've explored how rotating black holes drag spacetime around them like thick honey [7], creating regions where nothing can remain stationary relative to distant observers.

Through spacetime diagrams, we've learned to visualize geometries that exist beyond our three-dimensional experience [11], seeing how the singularity at the center of a black hole is not a place but a moment in time [5]. The waterfall model has given us an intuitive way to understand how spacetime itself can flow like a river [15], carrying objects along in its current. And we've pushed the boundaries of physics to explore wormholes and exotic matter [17], discovering the delicate balance between mathematical possibility and physical reality.

Perhaps most remarkably, all of these strange phenomena emerge naturally from Einstein's field equations – a set of mathematical relationships that connect the geometry of spacetime with the distribution of matter and energy [1]. The equations don't just describe black holes; they predict their existence and tell us exactly how they should behave. Every bizarre effect we've discussed is not an ad hoc addition to the theory but an inevitable consequence of the fundamental principles of general relativity.

The experimental confirmation of these predictions has been one of the great triumphs of modern physics. From the bending of light during solar eclipses to the detection of gravitational waves from colliding black holes [3], observation after observation has confirmed Einstein's theory in ever more extreme regimes. The recent images of black holes captured by the Event Horizon Telescope [21] have given us direct visual evidence of these cosmic monsters, showing the glowing accretion disk and the dark shadow of the event horizon exactly as Einstein's equations predict.

Yet for all our progress in understanding black holes, many mysteries remain. The nature of the singularity at the center of a black hole continues to elude us [5]. Our current theories suggest that the curvature of spacetime becomes infinite at the singularity, but this likely indicates the breakdown of general relativity rather than a true physical infinity. A complete theory of quantum gravity – one that unifies Einstein's theory with quantum mechanics – will probably be needed to understand what really happens at the center of a black hole.

The information paradox presents another deep puzzle [6]. If information falling into a black hole is preserved (as quantum mechanics suggests it must be), how does it escape when the black hole evaporates through Hawking radiation [14]? This question has led to new ideas about the nature of spacetime itself, including the holographic principle and the suggestion that the information might be encoded on the surface of the event horizon rather than in the interior.

The study of black holes has also revealed unexpected connections between seemingly disparate areas of physics [6]. The laws of black hole thermodynamics show that these gravitational objects behave like thermodynamic systems, with temperature and entropy. The AdS/CFT correspondence suggests deep connections between gravity and quantum field theory [20]. The ER=EPR conjecture proposes that wormholes and quantum entanglement might be different aspects of the same phenomenon.

These connections hint at a deeper unity underlying the laws of physics – a suggestion that gravity, quantum mechanics, and thermodynamics might all be different facets of a more fundamental theory. Black holes, as the most extreme gravitational objects in the universe, provide a unique laboratory for exploring these connections and testing our understanding of the fundamental laws of nature.

The practical implications of black hole physics extend far beyond academic curiosity. The GPS satellites that guide us through our daily travels must account for gravitational time dilation to maintain their accuracy [2]. The detection of gravitational waves has opened up an entirely new window on the universe [3], allowing us to observe cosmic events that are invisible to traditional telescopes. The study of black holes at the centers of galaxies helps us understand how these massive structures form and evolve over cosmic time.

Looking to the future, black hole physics promises to remain at the forefront of fundamental research. New gravitational wave detectors will allow us to observe black hole mergers with unprecedented precision [3], testing Einstein's theory in the most extreme gravitational fields in the universe. Advanced telescopes will provide ever more detailed images of black holes [21], revealing the dynamics of matter in the strongest gravitational fields known.

The quest for a theory of quantum gravity continues to be driven largely by the need to understand black holes. Whether this theory takes the form of string theory, loop quantum gravity, or something entirely new, it will need to explain what happens at the singularity and resolve the information paradox [6]. The answers to these questions may revolutionize our understanding of space, time, and reality itself.

Perhaps most importantly, the study of black holes reminds us of the power of mathematical reasoning and theoretical physics [1]. Einstein developed his theory of general relativity through pure thought, using mathematical consistency and physical principles as his guide. The theory predicted the existence of black holes decades before they were observed, and it continues to make predictions that are confirmed by increasingly sophisticated experiments.

This success illustrates one of the most remarkable aspects of physics: the ability of mathematical theories to reveal hidden aspects of reality [1]. The equations don't just describe what we observe; they predict phenomena that we haven't yet seen and guide us toward new discoveries. In the case of black holes, the mathematics has consistently been ahead of observation, pointing the way toward new phenomena and deeper understanding.

As we continue to explore the universe with ever more powerful instruments and ever more sophisticated theories, black holes will undoubtedly continue to surprise us. These cosmic monsters, born from the collapse of massive stars, represent some of the most extreme conditions in the universe. They challenge our understanding of space and time, push the boundaries of our theories, and reveal the deep connections between seemingly disparate areas of physics.

The strange things that happen when you follow Einstein's math are not just mathematical curiosities – they're real features of the universe we inhabit [1]. Time really does slow down in strong gravitational fields. Space really is curved by the presence of matter and energy. Black holes really do exist, and they really do behave in the bizarre ways that Einstein's equations predict.

In a universe where such wonders are possible, where the fabric of spacetime can be twisted into knots and where time itself can be stretched like taffy, we're reminded that reality is far stranger and more beautiful than our everyday experience suggests. The mathematics of general relativity has opened our eyes to this hidden reality [1], revealing a cosmos where the impossible becomes inevitable and where the deepest mysteries of existence play out on the grandest scales imaginable.

As we stand on the threshold of new discoveries in gravitational physics, quantum mechanics, and cosmology, the lessons learned from black holes will continue to guide us. These cosmic laboratories, where the laws of physics are pushed to their limits, will help us understand not just the nature of gravity and spacetime, but the fundamental structure of reality itself. In following Einstein's math, we've discovered that the universe is far more wonderful than we ever dared to imagine – and we've only just begun to explore its mysteries.

This exploration of black hole physics is based on our current understanding of general relativity and quantum mechanics. As our knowledge continues to evolve, some of the ideas presented here may be refined or replaced by new insights. The beauty of science lies not in having all the answers, but in the ongoing quest to understand the deep mysteries of the universe.

This video was the inspiration behind this post; highly recommend following the Veritasium Channel

References

[1] Einstein, A. (1915). "Die Feldgleichungen der Gravitation" (The Field Equations of Gravitation). Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften, 844-847. Available at: https://einsteinpapers.press.princeton.edu/vol6-trans/110

[2] NASA Blueshift. (2015). "100 Years of General Relativity." Available at: https://asd.gsfc.nasa.gov/blueshift/index.php/2015/11/25/100-years-of-general-relativity/

[3] LIGO Scientific Collaboration. (2016). "Observation of Gravitational Waves from a Binary Black Hole Merger." Physical Review Letters, 116, 061102. Available at: https://www.ligo.caltech.edu/page/what-are-gw

[4] Schwarzschild, K. (1916). "Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie" (On the Gravitational Field of a Point Mass According to Einstein's Theory). Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften, 189-196. Available at: https://arxiv.org/abs/physics/9905030

[5] Penrose, R. (1965). "Gravitational Collapse and Space-Time Singularities." Physical Review Letters, 14, 57-59. Available at: https://arxiv.org/abs/1410.5226

[6] Bekenstein, J. D. (1973). "Black Holes and Entropy." Physical Review D, 7, 2333-2346. Available at: https://link.aps.org/doi/10.1103/PhysRevD.7.2333

[7] Kerr, R. P. (1963). "Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics." Physical Review Letters, 11, 237-238. Available at: https://link.aps.org/doi/10.1103/PhysRevLett.11.237

[8] Lense, J., & Thirring, H. (1918). "Über den Einfluss der Eigenrotation der Zentralkörper auf die Bewegung der Planeten und Monde nach der Einsteinschen Gravitationstheorie." Physikalische Zeitschrift, 19, 156-163. Available at: https://en.wikipedia.org/wiki/Frame-dragging

[9] Everitt, C. W. F., et al. (2011). "Gravity Probe B: Final Results of a Space Experiment to Test General Relativity." Physical Review Letters, 106, 221101. Available at: https://link.aps.org/doi/10.1103/PhysRevLett.106.221101

[10] Penrose, R. (1969). "Gravitational Collapse: The Role of General Relativity." Rivista del Nuovo Cimento, 1, 252-276. Available at: https://ui.adsabs.harvard.edu/abs/1968physics...3025O/abstract

[11] Penrose, R. (1963). "Asymptotic Properties of Fields and Space-Times." Physical Review Letters, 10, 66-68. Available at: https://www.einstein-online.info/en/spotlight/the-singularity-theorem/

[12] Kruskal, M. D. (1960). "Maximal Extension of Schwarzschild Metric." Physical Review, 119, 1743-1745. Available at: https://ncatlab.org/nlab/show/Penrose+singularity+theorem

[13] Einstein, A., & Rosen, N. (1935). "The Particle Problem in the General Theory of Relativity." Physical Review, 48, 73-77. Available at: https://en.wikipedia.org/wiki/Wormhole

[14] Hawking, S. W. (1974). "Black Hole Explosions?" Nature, 248, 30-31. Available at: https://www.nature.com/articles/248030a0

[15] Hamilton, A. J. S., & Lisle, J. P. (2008). "The River Model of Black Holes." American Journal of Physics, 76, 519-532. Available at: https://arxiv.org/abs/gr-qc/0411060

[16] Unruh, W. G. (1981). "Experimental Black-Hole Evaporation?" Physical Review Letters, 46, 1351-1353. Available at: https://jila.colorado.edu/news-events/articles/space-river

[17] Morris, M. S., & Thorne, K. S. (1988). "Wormholes in Spacetime and Their Use for Interstellar Travel: A Tool for Teaching General Relativity." American Journal of Physics, 56, 395-412. Available at: https://www.pas.rochester.edu/~tim/introframe/AmJPhysBlackHoles.pdf

[18] Ford, L. H., & Roman, T. A. (1995). "Quantum Field Theory Constrains Traversable Wormhole Geometries." Physical Review D, 53, 5496-5507. Available at: https://inspirehep.net/literature/276997

[19] Hawking, S. W. (1992). "Chronology Protection Conjecture." Physical Review D, 46, 603-611. Available at: https://physics.stackexchange.com/questions/846148/which-features-of-the-morris-thorne-wormhole-require-exotic-matter

[20] Maldacena, J., & Susskind, L. (2013). "Cool Horizons for Entangled Black Holes." Fortschritte der Physik, 61, 781-811. Available at: https://www.worldscientific.com/doi/10.1142/S021988782150170X

[21] Event Horizon Telescope Collaboration. (2019). "First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole." The Astrophysical Journal Letters, 875, L1. Available at: https://eventhorizontelescope.org/