Based on the brilliant explanation by Grant Sanderson (3Blue1Brown) in his video "But what is quantum computing? (Grover's Algorithm)"

If you've ever heard someone explain quantum computing, chances are you've encountered the most seductive and misleading explanation in all of computer science: "Quantum computers are so powerful because they can try all possible solutions at the same time!" It sounds magical, doesn't it? Like having a computer that splits into parallel universes, each one testing a different answer, then somehow brings back the correct result from whichever universe found it first.

Here's the thing: that explanation is not just wrong—it's spectacularly wrong. And understanding why it's wrong is the key to understanding what quantum computers actually do, which is far more subtle, far more beautiful, and arguably far more mind-bending than the parallel universe fairy tale.

This misconception is so pervasive that Grant Sanderson, the mathematical wizard behind the YouTube channel 3Blue1Brown, dedicated an entire 37-minute video to dismantling it and building up the real story from the ground up. In his characteristically elegant style, Sanderson doesn't just tell us what quantum computers do—he shows us the mathematics that makes it possible, building up to one of the most important quantum algorithms ever discovered: Grover's algorithm.

The Great Quantum Misconception

Let's start by understanding why the "parallel processing" explanation is so appealing and so wrong. When most people first hear about quantum superposition—the idea that a quantum particle can be in multiple states simultaneously—their minds naturally jump to a classical analogy. If a quantum bit (or "qubit") can be both 0 and 1 at the same time, then surely a quantum computer with many qubits can explore all possible combinations of 0s and 1s simultaneously, right?

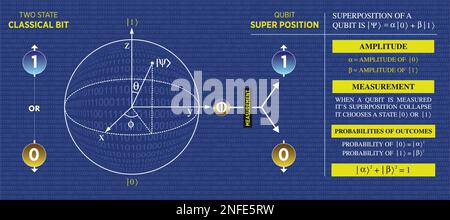
The fundamental difference between classical bits and quantum qubits goes far deeper than just "being in multiple states at once"

This intuition feels so natural that it's become the go-to explanation for quantum computing's potential power. The problem is that it fundamentally misunderstands what quantum computers can and cannot do. As Chris Ferrie, a quantum physicist and science communicator, puts it: "The most fantastical, and hence the most popular, explanation of quantum computing is that it happens simultaneously in parallel worlds."

The reality is more nuanced. Quantum computers don't solve problems by trying all solutions in parallel—they solve problems by manipulating the mathematical structure of quantum states in ways that classical computers simply cannot. To understand this, we need to dive into the mathematical heart of quantum computing: state vectors.

Enter the State Vector: The Real Language of Quantum Computing

Here's where Sanderson's explanation becomes truly illuminating. Instead of relying on fuzzy analogies about cats being dead and alive, he cuts straight to the mathematical core: quantum states are vectors in a complex vector space.

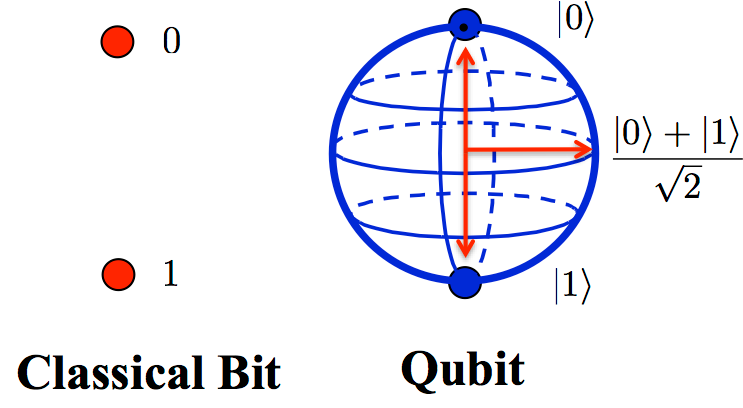
Quantum states can be represented as vectors in a mathematical space, where each possible outcome has an associated amplitude

Think of it this way: in classical computing, a bit is either 0 or 1. Period. But in quantum computing, a qubit is described by a mathematical object called a state vector, which contains information about the probability amplitudes for all possible measurement outcomes. These amplitudes are complex numbers—numbers that have both a magnitude and a phase—and they're the secret sauce that makes quantum computing work.

When you have multiple qubits, the state vector doesn't just grow linearly—it grows exponentially. Two qubits require a 4-dimensional vector, three qubits require an 8-dimensional vector, and n qubits require a 2^n-dimensional vector. This exponential scaling is real, and it's where quantum computers get their potential power. But—and this is crucial—having an exponentially large state vector doesn't mean you can extract exponentially much information from it.

This is the first key insight that demolishes the "parallel processing" myth: quantum computers can manipulate exponentially large amounts of information, but they can only extract a limited amount of classical information when you measure the system. The art of quantum algorithm design lies in manipulating these amplitudes in clever ways so that when you finally measure the system, the right answer has a high probability of appearing.

The Quantum Function: Flipping Signs Instead of Returning Values

Now we come to one of the most elegant insights in Sanderson's explanation. In classical computing, functions take inputs and return outputs. A search function might take a list and a target value, then return "true" if the target is found and "false" otherwise. Simple, straightforward, and utterly classical.

Quantum functions work differently. Instead of returning true or false, a quantum function manipulates the state vector. Specifically, when a quantum function "recognizes" the correct input, it doesn't return true—it flips the sign of that input's amplitude in the state vector.

This might sound like a trivial difference, but it's actually profound. By flipping the sign instead of returning a value, the quantum function preserves all the quantum information in the system while still "marking" the correct answer. This sign flip becomes the foundation for everything that follows.

Quantum operations manipulate probability amplitudes rather than classical bits, allowing for fundamentally different computational approaches

Think of it like this: imagine you're in a vast library with millions of books, and you're looking for one specific book. A classical search would involve checking each book one by one until you find the right one. But a quantum search is more like having a magical librarian who can simultaneously whisper to every book in the library, and the right book responds by glowing slightly differently. The librarian doesn't tell you which book is glowing—you still have to look—but the glow makes it much more likely that you'll spot the right book quickly.

Grover's Algorithm: The Quantum Search That Actually Works

This brings us to the star of Sanderson's video: Grover's algorithm. Developed by Lov Grover in 1996, this algorithm represents one of the most important breakthroughs in quantum computing, and it perfectly illustrates how quantum computers actually achieve their speedup.

Grover's algorithm uses a combination of oracle queries and diffusion operations to amplify the probability of finding the correct answer

Grover's algorithm solves what computer scientists call the "unstructured search problem." Imagine you have a database with N entries, and exactly one of them satisfies some condition you're looking for. In classical computing, you'd have to check, on average, N/2 entries to find the right one. In the worst case, you might have to check all N entries.

Grover's algorithm can find the right entry in approximately √N steps. For a database with a million entries, that's the difference between checking 500,000 entries on average (classical) versus checking about 1,000 entries (quantum). That's not just an improvement—it's a fundamental speedup that no classical algorithm can match.

But here's the crucial point: Grover's algorithm doesn't work by "trying all solutions in parallel." Instead, it works by repeatedly applying two operations: the oracle (which flips the sign of the correct answer) and the diffusion operator (which performs a specific rotation in the state space).

The Geometric Beauty of Quantum Search

One of the most beautiful aspects of Sanderson's explanation is how he visualizes Grover's algorithm geometrically. Instead of getting lost in the exponential complexity of the full state space, he shows us that we can understand the algorithm by looking at just a two-dimensional slice of that space.

The geometric interpretation of Grover's algorithm shows how it rotates the state vector toward the correct answer

Picture a two-dimensional plane where one axis represents the "correct answer" direction and the other represents the "everything else" direction. The algorithm starts with the state vector pointing mostly toward the "everything else" direction—this represents the initial superposition where all answers are equally likely.

Each iteration of Grover's algorithm rotates this vector slightly toward the "correct answer" direction. The oracle operation reflects the vector across the "everything else" axis, and the diffusion operation reflects it across the average direction. The combination of these two reflections produces a rotation, and after approximately √N iterations, the vector points almost entirely toward the "correct answer" direction.

This geometric picture reveals something profound: Grover's algorithm doesn't succeed by exploring all possibilities simultaneously. It succeeds by systematically rotating the quantum state toward the correct answer through a carefully choreographed sequence of operations.

Why This Matters: The Real Power of Quantum Computing

Understanding how Grover's algorithm actually works helps us understand the real source of quantum computing's power. It's not about parallel processing or exploring multiple universes. It's about exploiting the mathematical structure of quantum mechanics to perform computations that are fundamentally impossible for classical computers.

The quadratic speedup that Grover's algorithm provides might not sound as exciting as the exponential speedups promised by other quantum algorithms like Shor's algorithm for factoring large numbers. But it's actually quite remarkable. This speedup applies to any problem where you can quickly verify a solution but finding the solution requires search. That includes a vast range of optimization problems, cryptographic applications, and machine learning tasks.

Moreover, Grover's algorithm is provably optimal for unstructured search. This isn't just the best quantum algorithm we've found so far—it's the best quantum algorithm that can possibly exist for this type of problem. Charles Bennett, Ethan Bernstein, Gilles Brassard, and Umesh Vazirani proved that any quantum algorithm for unstructured search must make at least Ω(√N) queries to the oracle. Grover's algorithm achieves this bound, making it asymptotically optimal.

The Subtle Art of Quantum Advantage

This brings us to a deeper understanding of what quantum computers can and cannot do. The popular misconception suggests that quantum computers are universally faster than classical computers, but the reality is more nuanced. Quantum computers provide advantages for specific types of problems that have particular mathematical structures that quantum mechanics can exploit.

For Grover's algorithm, that structure is the ability to create and manipulate superpositions of all possible inputs, combined with the ability to perform operations that depend on whether a particular input satisfies the search condition. The quantum advantage emerges from the interference between different amplitude components in the superposition—some amplitudes cancel out while others reinforce, gradually concentrating the probability on the correct answer.

This is fundamentally different from classical parallel processing. In classical parallel computing, you might run multiple processors simultaneously, each checking different parts of the search space. But each processor is still fundamentally limited to classical operations, and the total number of operations across all processors still scales linearly with the problem size.

Quantum computing transcends this limitation not by doing more operations in parallel, but by doing fundamentally different types of operations that have no classical analog. The interference effects that make Grover's algorithm work simply don't exist in classical physics.

The Broader Implications: What This Means for the Future

Understanding the real mechanism behind quantum computing helps us set realistic expectations for the technology's future. Quantum computers won't replace classical computers for everyday tasks like browsing the web or editing documents. Instead, they'll serve as specialized tools for specific problems where quantum effects can provide genuine advantages.

The applications are still profound. Grover's algorithm can speed up database searches, optimization problems, and certain machine learning tasks. More broadly, the principles behind Grover's algorithm—amplitude amplification and quantum interference—form the foundation for many other quantum algorithms.

In cryptography, Grover's algorithm has immediate implications. It effectively halves the security level of symmetric encryption schemes. A 256-bit encryption key, which would take classical computers an impractically long time to break by brute force, could be broken by a quantum computer running Grover's algorithm in roughly 2^128 operations—still a large number, but within the realm of possibility for a sufficiently powerful quantum computer.

This has led cryptographers to develop "post-quantum" encryption schemes that remain secure even against quantum attacks. The transition to post-quantum cryptography is already underway, driven in part by our understanding of algorithms like Grover's.

The Mathematical Beauty Behind the Mystery

Perhaps the most remarkable aspect of Sanderson's explanation is how it reveals the mathematical beauty underlying quantum computing. Far from being a collection of weird quantum effects that somehow produce computational speedups, quantum computing emerges as a natural and elegant extension of classical computation into the realm of complex vector spaces.

The state vector formalism that describes quantum systems is the same mathematical framework used in many other areas of physics and engineering. The operations that quantum computers perform—unitary transformations of complex vectors—are well-understood mathematical objects with rich geometric interpretations.

This mathematical foundation gives us confidence that quantum computing is not just a clever trick, but a fundamental new way of processing information. As we develop better quantum hardware and discover new quantum algorithms, we're not just building faster computers—we're exploring new regions of the mathematical landscape of computation itself.

Looking Forward: The Quantum Future

As we stand on the brink of the quantum computing era, understanding the real mechanisms behind quantum algorithms becomes increasingly important. The hype around quantum computing often focuses on dramatic claims about exponential speedups and revolutionary breakthroughs. While some of these claims are justified, the reality is more subtle and, in many ways, more interesting.

Quantum computers won't solve all our computational problems, but they will solve some problems in fundamentally new ways. Grover's algorithm, with its elegant geometric interpretation and provable optimality, serves as a perfect example of what quantum computing can achieve when we move beyond the misconceptions and embrace the mathematical reality.

The next time someone tells you that quantum computers work by "trying all solutions in parallel," you can share the real story: quantum computers work by manipulating the mathematical structure of quantum states in ways that have no classical analog. They achieve their speedups not through brute force parallelism, but through the subtle and beautiful mathematics of quantum interference.

And that, as Grant Sanderson would undoubtedly agree, is far more wonderful than any parallel universe explanation could ever be.

Created by Bogdan Cristei and Manus AI

This blog post is based on the excellent video "But what is quantum computing? (Grover's Algorithm)" by Grant Sanderson (3Blue1Brown). You can watch the original video at: https://www.youtube.com/watch?v=RQWpF2Gb-gU

For more insights into quantum computing and mathematics, visit 3Blue1Brown's channel and website at https://www.3blue1brown.com